Homeomerías...

El universo es caótico y compacto, de una belleza fascinante y vertiginosa. El orden se da sólo en pequeñas islas rodeadas de impredictibilidad, como bien sabía ya Anselmo de Canterbury, para quien la razón estaría rodeada por un mar de irracionalidad.

¿Qué es pues el caos? Nada sino nuestra incapacidad para medir, para predecir comportamientos de variables; no otra cosa significa la palabra irracional. El cambio de perspectiva radica en aceptar que no es el orden sino el caos aquello que domina la composición total del universo, es su inestabilidad y no lo contrario su rasgo dominante. Para reproducir los fenómenos naturales o los objetos del mundo debemos echar mano de una geometría que no posee una unidad de medida absoluta, sino una que se adapta a la perspectiva escogida, ya sea para mirar desde el satélite, para observar a ojo desnudo o para acercarnos con el más potente microscopio. Las 3 dimensiones con las que se creía reproducir el mundo fielmente, no son más que un corsé demasiado estrecho. El detalle y la riqueza del mundo quedan mejor expresados mediante iteraciones que utilizan como base una dimensión fraccionaria. ¿Cuántos entienden el significado de este desplazamiento en el concepto de dimensión?

La tesis de grado del geógrafo inglés Mandelbrot versa sobre la imposibilidad de medir la costa de Inglaterra. Dicha medición depende en absoluto del lugar desde donde la hacemos. La Tierra vista desde el Sol parece un punto; desde la Luna, una esfera, desde su superficie nos parece plana. Si nos zambullimos en el detalle de sus rocas, etc., etc., etc., se nos abre de nuevo un horizonte inalcanzable.

Nuestro viaje comienza muy alto sobre el plano de los números complejos. (fig. 1)

La figura que se observa es el llamado Conjunto de Mandelbrot, generado por un computador a partir de la función compleja z² + C, en la que z pertenece al conjunto de los números complejos y C es una constante compleja cualquiera. El computador itera la operación y pinta de blanco aquellos números que se mantienen dentro de un rango fijo, de negro aquellos que lo trangreden y de algún otro color aquellos que conforman el conjunto.

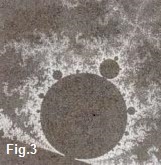
Si nos acercamos hasta una distancia que establecemos como el tamaño normal de la figura, observamos la aparición de zonas intermedias. (fig. 2), de lo que podríamos llamar su atmósfera. Entremos en ella y concentrémosnos en la forma verrugosa circular. (fig. 3) acercándonos a su litoral (fig. 4). Las orillas están llenas de rizos y simétricamente las recorre un filamento que llama nuestra atención. Pongamos la lupa sobre alguna parte de él. (fig. 5) y nos sorprenderá la visión de un conglomerado de luces  de forma florescente, cuyos capullos encierran una semilla espectacular y que sólo descubrimos al zambullirnos en la flor. (fig. 6) 

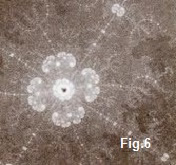
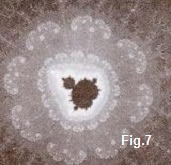
Lo que tenemos ante la vista es el llamado Nanomandelbrot, una réplica exacta de la figura que fue nuestro punto de partida, sólo que millones de veces más pequeña. (fig.7)

Sin un computador no habríamos podido jamás descubrir estas regiones llenas de belleza y misterio, un mundo de formas geométricas no platónicas.

Existe de hecho una prueba formal del carácter compacto del espacio funcional generado por la expresión compleja del conjunto de Mandelbrot, pero esta posibilidad de contemplación directa de la coherencia interna linda con la maravilla y le habla directamente al espíritu.